Play With Lua!

In this post, and the following posts in this series, I aim to fix something that’s bothered me for a while: writing a parser in Lua isn’t very approachable. In C you have the excellent chapter in The Unix Programming Environment (probably the best book on programming ever written) about how to use Lex and Yacc. For Ruby there’s the excellent Dhaka gem, as well as Racc, both of which work a lot like Yacc / Bison. There’s also Antlr, which seems to speak to every language except Lua.

Meanwhile Lua has LPeg, which is used nothing like Yacc, and tutorials are thin on the ground. So, I want to change that. This is going to be about how to make a toy programming language in Lua, in three parts. I’m going to loosely follow what the Lex / Yacc chapters of The Unix Programming Environment do, and we’ll end up with the same language.

Let’s begin.

Getting started with LPeg

Covering how to build and install LPeg is going to be impossible to do for every system, and out of scope anyway, so let’s just assume you have already installed it somehow. You can verify that you have it like this:

lpeg = require 'lpeg'
print( type(lpeg) == 'table')

Now that we have it loaded, let’s start making a parser. Parsers are made up of patterns, which are objects (userdata) that match certain things in strings. Each pattern has a set of things that it will match, and a match method that takes a string and returns whether it matches or not.

The simplest possible pattern is one that matches a literal string:

p = lpeg.P("apple")

This pattern will match the string “apple” and nothing else:

p:match("bob") -- nil
p:match("apple") -- 6

We get a nil back if it doesn’t match, and a 6 back if it does, because 6 is the index in the string immediately following the match. This pattern will also match anything that starts with “apple”:

p:match("appletree") -- 6

It knows how to parse “apple” but what comes after it it doesn’t match, so it leaves it alone.

You can also combine patterns together:

p = lpeg.P("apple") * lpeg.P("tree")

“Multiplying” two patterns means “match this pattern, followed by this one.” So, this would match “apple” followed by “tree”. “Adding” them means to match either one or the other, so this matches either “apple” or “tree”:

p = lpeg.P("apple") + lpeg.P("tree")
p:match('apple') -- 6
p:match('tree') -- 5
p:match('bob') -- nil
p:match('appletree') -- 6

The last one matches because the “tree” part is treated as unrecognized input, just as above. If we want it to not match, we have to say “match ‘apple’ or ‘tree’ followed by the end of the string.” We can do that easily, because lpeg.P can also take a number, and interprets it as “match exactly this many characters, no matter what they are.” If you pass it -1, it matches the end of the string:

p = (lpeg.P("apple") + lpeg.P("tree")) * lpeg.P(-1)
p:match('appletree') -- nil

Finally, “exponentiating” a pattern with a number matches repetitions of that pattern:

-- match at least 3 'a' characters, followed by a 'b', then end of string:
p = lpeg.P("a")^3 * "b" * -1
p:match('ab') -- nil
p:match('aaab') -- 5
p:match('aaabc') -- nil

(note that we can use literal strings and numbers, and it’s just as if we called lpeg.P.

More complicated patterns

So far there’s nothing we can’t do with ordinary string expressions. But, patterns can be combined in other ways. Here’s a pattern that matches a number:

number = lpeg.P('-')^-1 *
         lpeg.R('09')^0 *
         (
             lpeg.P('.') *
             lpeg.R('09')^0
         )^-1 *
         -1

I’ve split it into multiple lines to make it clearer. Let’s walk through this: we start by having “-” matched at most 1 time (exponentiating by a negative means “repeated at most,” exponentiating by a positive or 0 means “repeated at least”). This allows us to have negative numbers. Then, we have at least 0 repetitions of lpeg.R('09'): this is a “range” pattern, which matches any character between the two, so, any digit. This is the integer part of the number.

Then there’s a block wrapped up in parentheses: ( ... )^-1. Again, we’re repeating this portion at most one time, and that portion is a “.” followed by another series of digits. Finally, we match end-of-string.

So, testing this, we see that it matches various numbers:

number:match('53')
number:match('-17')
number:match('5.02')
number:match('.3')
number:match('7.')

Captures

Up until now, we’ve been concerned with seeing whether a given string matches a pattern. But that’s something we could do (with this example anyway) using a regular expression. In order to make any sort of useful parser we’ll need to extract portions of the string, while recognizing what they are. In this case, we’ll want to extract the integer part of the number, the fractional part, and whether there’s a negative sign.

We do this with an LPeg concept called captures. The simplest capture is to just have the pattern return, instead of a string index, some portion of the string:

number = lpeg.C( lpeg.P('-')^-1 ) *
         lpeg.C( lpeg.R('09')^0 ) *
         (
             lpeg.P('.') *
             lpeg.C( lpeg.R('09')^0 )
         )^-1 *
         -1

You’ll notice we’ve wrapped three portions of our pattern in lpeg.C. This creates a capture, by adding whatever is wrapped in lpeg.C to the return values of match. It makes more sense if you try it:

sign, ipart, fpart = number:match("-37.7")

sign, ipart, and fpart are now “-“, “37”, and “7” respectively: instead of returning 6 (the index right after the match), a pattern with captures returns the captures.

The other handy thing we can do here is to use a function capture: “dividing” the pattern by a function will pass all the captures to that function, and then return what the function returns:

function parse_num(sign, ipart, fpart)
    return { negative = (sign=='-'),
             ipart = ipart,
             fpart = fpart }
end
 
number = lpeg.C( lpeg.P('-')^-1 ) *
         lpeg.C( lpeg.R('09')^0 ) *
         (
             lpeg.P('.') *
             lpeg.C( lpeg.R('09')^0 )
         )^-1 *
         -1 /
         parse_num
 
number:match("-7.2") -- {negative=true, ipart="7", fpart="2"}

Or, we could do it a little more simply by using tonumber:

number = lpeg.C(
           lpeg.P('-')^-1 *
           lpeg.R('09')^0 *
           (
               lpeg.P('.') *
               lpeg.R('09')^0
           )^-1 ) /
         tonumber
 
number:match("-7.2") -- -7.2

This will capture the whole thing at once, and feed it to a function that happens to be in the standard library that turns a string into a number.

Parsing simple expressions

Let’s make a calculator. For this first step, we’ll parse simple expressions consisting of two numbers and an operator: “2+2”, “3*-7.5”, and the like. Here’s a pattern that matches an expression, using the number pattern from above:

spc = lpeg.S(" \t\n")^0
expr = spc * number * spc * lpeg.C('+') * spc * number * spc * -1 +
       spc * number * spc * lpeg.C('-') * spc * number * spc * -1 +
       spc * number * spc * lpeg.C('*') * spc * number * spc * -1 +
       spc * number * spc * lpeg.C('/') * spc * number * spc * -1

This has a few things in it we haven’t explained. First, the spc pattern I’ve written will match whitespace but create no captures, so we can put random whitespace in the string to separate tokens. The spc pattern uses lpeg.S, which means “match any one of the characters in this string.”

If we feed a string to this, we’ll see it capture the two numbers and the operator:

expr:match("2 * 3") -- 2, '*', 3

Now it’s easy enough to make a function to evaluate these:

function eval(num1, operator, num2)
    if operator == '+' then
        return num1 + num2
    elseif operator == '-' then
        return num1 - num2
    elseif operator == '*' then
        return num1 * num2
    elseif operator == '/' then
        return num1 / num2
    else
        return num1
    end
end

And then, a REPL:

function repl(file)
    file = file or io.input()
    parser = expr / eval
    for line in file:lines() do
        print(parser:match(line))
    end
end

Call this on a filehandle (defaults to stdin) to read, evaluate, and print simple exprs.

Recursive grammars

Of course, these are very simple expressions: two terms and one operator. It would be a lot better if we could put in more complex expressions like “2 * 3 + 5”. We can do that by making the pattern recursive: an expr can be defined as a pattern that contains another expr. But in order to do that, we need to use something LPeg calls a grammar:

expr = lpeg.P{
    "EXPR";
    EXPR = ( lpeg.V("TERM") * lpeg.C( lpeg.S('+-') ) * lpeg.V("EXPR") +
             lpeg.V("TERM") ) / eval,
    TERM = ( lpeg.V("FACT") * lpeg.C( lpeg.S('/*') ) * lpeg.V("TERM") +
             lpeg.V("FACT") ) / eval,
    FACT = ( spc * "(" * lpeg.V("EXPR") * ")" * spc +
             number ) / eval
}

A grammar is made by passing a table to lpeg.P. The first element in the table is the name of a nonterminal, and it’s what we start by trying to match. All the rest define nonterminals. In order to reference a nonterminal, we use lpeg.V.

So, this says:

Start trying to match an EXPR. An EXPR is either a TERM plus-or-minus an EXPR, or it’s just a TERM by itself. When you see an EXPR, send it to eval.

A TERM is either a FACT multiply-or-divide a TERM, or a FACT by itself. Send these to eval also.

A FACT is either an EXPR in parentheses, or a number. These, too, get sent to eval.

When we match a string like “2 * (3 + 4)”, LPeg will parse it like this:

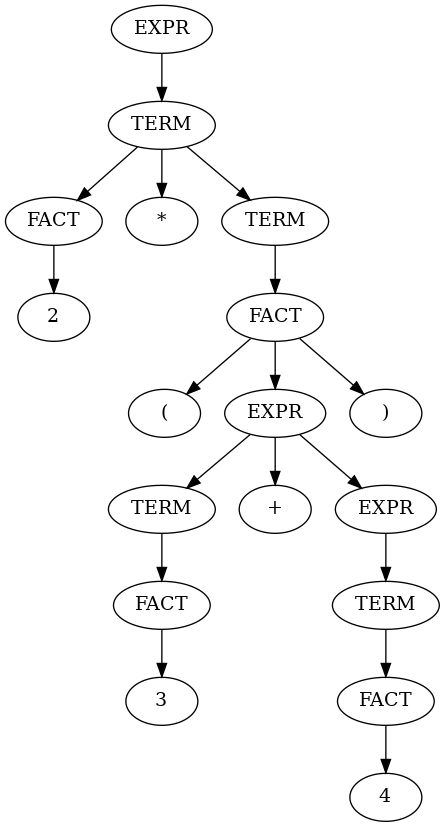
The reason we separate out EXPR, TERM, and FACT (expression, term, and factor) is that LPeg has no other way of assigning operator precedence: if an EXPR’s middle operator could be either a plus or a multiply, then “2+3*4” would generate the same tree structure as “2*3+4”. So, we have some extra internal nodes in there. If we wanted, we could eliminate a lot of them by having the rules not be recursive: EXPR could be a series of TERMs with operators, instead of a single TERM followed by an EXPR. That’s what the LPeg example has. However, I’m trying to closely follow what The Unix Programming Environment does, and demonstrate that recursion works.

Trying it out

Here are a few test cases that should prove this is parsing correctly:

1
(2)
1+2
2*3
2*3+1
2*(3+1)

If you try this out using the same repl function as before you’ll see they all work.

Next steps

At this point we have something about like the first version of the calculator in The Unix Programming Environment. The next step, which will be in the next post, will be to add variables and control structures.

As always, you can get the code from this post (for the final version of this parser) here.